326 replies to this topic

[kucalc]

There has been a lot of mathematical evidence showing that 0.999999999.... = 1 IS TRUE. In this whole entire thread, there has not been a single post showing some mathematical evidence that 0.99999999999..... does not equal one!

It must be true then that 0.99999999999.... equals 1.

[TacoFred]

Hm....kucalc, you may have been typing too fast, but there is no AP Western Civ. I'm glad that you are actually studying above the level of most US high school students, but as was said, the educational level of different schools are completely different. It's just that the range of educational system quality is very wide in the US (from VERY bad to VERY good) while in some countries, it is a smaller range (good to VERY good). The high school program that I'm in, Science and Engineering, is located within a school full of druggies and dealers, which is I believe a perfect example...

Moving onwards, I believe that it is pointless to further discuss whether 0.999...=1 since it cannot be incontrovertibly proven/unproven (though this discussion has been interesting, to say the least).

[kucalc]

Hm....kucalc, you may have been typing too fast, but there is no AP Western Civ.

The textbook I'm using is called Western Civilization, 4th Edition Comprehensive Volume by Spielvogel. Western civilization is a term that people most most often associate with Europe or Europe's culture and it's influence. It's actually called AP European History. Sorry for the confusion, thought that people would know what I meant...

[eew]

There has been a lot of mathematical evidence showing that 0.999999999.... = 1 IS TRUE. In this whole entire thread, there has not been a single post showing some mathematical evidence that 0.99999999999..... does not equal one!

It must be true then that 0.99999999999.... equals 1.

Can you show me the matamatical evidence?

[Menno]

1/3=0,33333333->infinite

3x1/3=1,0

3x0,333333333->infinite=0,9999999999->infinite

but that is no evidence, it is just why fractions are invented in the first place

[TyYann]

Moving onwards, I believe that it is pointless to further discuss whether 0.999...=1 since it cannot be incontrovertibly proven/unproven (though this discussion has been interesting, to say the least).

Well, it has been proven incontrovertibly that 0.999...=1. And not only on this forum. The problem is that people don't accept the proofs.
Here is why :
http://www.casiocalc...amp;#entry37287

As said by Kucalc, it has been proven that 0.999...=1 is true in several different ways, but not once that it is false.
Yet, people won't admit it.

[protoman no one]

dear casiocalc people (and kucalc, of course )
i must admit that i was wrong (but i?m still not sure), 0.999999999............=1, but take this "proof"
and "definition" (of course, i know they are not matematically rigorous )
definition: 2 real numbers are the same if they decimal representation are the same ( )
but:
1=0.99999999999.........
1=1.00000000000.........(why not?)
then 1=1 if 0.999999999......=1.00000000000.....
but 0.9<>1.0, 0.99<>1.00,........, 0.999999......<>1.000000000......then 0.99999999.....<>1!!??
then, can you explain me, please, where is my failure suposing that 0.9999999<>1???
bye people, and.....what do you think of a version of a megaman game on casio??? (i?m triying to program it........so post any coments
protoman no one

[vanhoa]

2 real numbers are the same if their decimal representation are the same does not equa to 2 real numbers are not the same if their decimal representation are not the same.

You wrong.

[kucalc]

(and kucalc, of course )

Lol.

then, can you explain me, please, where is my failure suposing that 0.9999999<>1???

Well, of course 0.9999999 absolutely does not equal 1. I think however you mean to put 0.9999999... You forgot the .... to represent the infinite.

bye people, and.....what do you think of a version of a megaman game on casio??? (i?m triying to program it........so post any coments

Start a thread for this in the CASIO CFX/AFX/FX subforum. If you would like, may I join your Mega Man project? I can help you program the game in C for the AFX. Are you good in doing graphics?

[protoman no one]

Lol.
Well, of course 0.9999999 absolutely does not equal 1. I think however you mean to put 0.9999999... You forgot the .... to represent the infinite.
Start a thread for this in the CASIO CFX/AFX/FX subforum. If you would like, may I join your Mega Man project? I can help you program the game in C for the AFX. Are you good in doing graphics?

yes you?re right. lol
answering to your mega question: yup, if you want . i dragged some sprites, but i?m having problems with stagemaps (i think they are very bigger (memory talking, of course) and i?m learning (slooooooower, take that on mind) programing in x86 assembly language (i understand that nec v30mx instruction set is compatible with intel x86 ). sooooooo, what do you think?? maybe we need to do some "level packs", and improve a save-state system, because you know, megaman levels are loooong, and calc?s memory is notttt
and, i?m thinking on some cinema displays for the game......

for vanhoa:
in my proof i said: "SUPOSING that 2 real numbers have the same decimal representation"
NOTE THAT I?M SUPOSING, I?M NOT TALKING ABOUT THAT IS TRUE
of course, i?m not a dummie (or hippie, yuppie, sleepie, stupid-ie or any kind of "ie" you could think )
bye bye

[TyYann]

Link already posted. Read the whole thread next time...

[kevinator9]

On my ClassPad, 10 9's (thats: 0.9999999999) = 0.9999999999 11 9's (thats: 0.99999999999) = 1, Although why do we use .999999999999 when we can use fractions? 99999999999/100000000000 does not, I believe equal 1.

I think you should make a Megaman game (I love Megaman it is wicked!) and maybe you could release a ClassPad version? (as that is the only casio calc I have)

[TyYann]

On my ClassPad, 10 9's (thats: 0.9999999999) = 0.9999999999 11 9's (thats: 0.99999999999) = 1,

Because with eleven 9s, your ClassPad rounds the number.

Although why do we use .999999999999 when we can use fractions? 99999999999/100000000000 does not, I believe equal 1.

Because we are speakink here about 0.99999999... which means an infinite series of 9s after the "..."

[kucalc]

kevinator9, I wonder if they have taught you at school how to convert a repeating decimal into a fraction. If not, Google "convert a repeating decimal into a fraction": http://www.google.co...G=Google Search

[protoman no one]

On my ClassPad, 10 9's (thats: 0.9999999999) = 0.9999999999 11 9's (thats: 0.99999999999) = 1, Although why do we use .999999999999 when we can use fractions? 99999999999/100000000000 does not, I believe equal 1.

I think you should make a Megaman game (I love Megaman it is wicked!) and maybe you could release a ClassPad version? (as that is the only casio calc I have)

i?m still working on it. first, i will release it on afx (i love that calc), next, if kucalc helps me, i will convert the code for the new fx 9860 sd (i don?t know how to program in assembly on it), next i will release it in mlc language, and finally if somebody helps me i will make a classpad version.
have a nice day

[kucalc]

protoman #1, welcome back. I thought you were gone forever. I was losing hope in the Megaman game.

I'll try to help and do my best in putting Megaman for the AFX and fx-9860. Have you finished drawing the sprites?

[kevinator9]

Sorry about that...guess I was sorta wrong

[protoman no one]

protoman #1, welcome back. I thought you were gone forever. I was losing hope in the Megaman game.

only over my dead body

I'll try to help and do my best in putting Megaman for the AFX and fx-9860. Have you finished drawing the sprites?

yup/nop................ok, but i still having problems with stage bitmaps.
see you later.......when my first demo is finished........

[kucalc]

Post the MegaMan update in the MegaMan thread in the General section of this forum.

[sayuke]

it does = 1
think of it this way
.999999999.....
= 9/10 + 9/100 + 9/1000.....
so you could say each term equals
Tn = (9/10)*(1/10)^n
which is a simple geometric sequence for which the sum to infinity is
Soo = (9/10) * (1/(1-1/10))
Soo = (9/10) * (10/9) = 1

or for you casio engineers you could of course throw the sum into your classpad from 0 to infinity, and it will also tell you 1

[kucalc]

If this .9999999...=1 issue was in a U.S. court it would be officially declared throughout the country that 0.99999... = 1

There's already so much evidence proving that 0.99999... = 1 and it's just getting repeated over and over again.

[verena]

There has been a lot of mathematical evidence showing that 0.999999999.... = 1 IS TRUE. In this whole entire thread, there has not been a single post showing some mathematical evidence that 0.99999999999..... does not equal one!

It must be true then that 0.99999999999.... equals 1.

Oh... OK, let's see if our Casios can provide us with an answer.

Use any scientific casio that has hyperbolic functions.

Type INV HYP TAN 0.9999999999999999.... (as many nines as you want)
Type = or EXE, whatever is there. You will get an answer.

Now, Type INV HYP TAN 1
Type = or EXE, whatever it has. You will get "E", "Math Error" (on my fx-991ES) or similar.

Is this mathematical enough ?
1 is NOT equal to 0.9999.... no matter the number of 9's.

[kucalc]

Oh... OK, let's see if our Casios can provide us with an answer.

The problem with calculators is that you can't type in an infinite number of digits. You would have to spend enternity, non stop, punching in the digits. Thus you can't use a calculator to determine whether this proof is false. Calculators usually only hold up to 100 digits at the most. 100 does not equal infinity. If you've read the posts on the previous pages, it has been said numerous times and everyone has agreed, you can't use a calculator for this problem because a calculator can't hold infinity digits.

... means going on forever, always repeating the 9's never stop.

1 is NOT equal to 0.9999.... no matter the number of 9's.

The problem again is infinity is not a number. Infinity goes on forever and forever. Can you type 9 into your calculator forever? I don't think so.

Is this mathematical enough ?

You haven't really shown us any mathematical proof. All you've done is shown that a calculator doesn't hold an infinite amount of digits.

[verena]

The point is simply that the inverse tangent hyperbolic of 1 does not exist, and the inverse tangent hyperbolic of 0.999999... does, therefore 1 is not equal to 0.999999.

the inverse hyperbolic tangent of (0.9999999...) = infinity

the inverse hyperbolic tangent of (1) = undefined

Is this mathematical enough, then ?

[kucalc]

the inverse hyperbolic tangent of (0.9999999...) = infinity

Correct.

the inverse hyperbolic tangent of (1) = undefined

Wrong.

The inverse hyperbolic tangent of 1 is also infinity, NOT undefined.

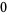
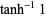
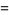
Go to this page, scroll down and look at equation 6: http://mathworld.wol...licTangent.html

Who taught you that the atanh of 1 is undefined? Did you use a calculator? I already said don't use the calculator.

The mistakes you're doing are just adding more proof that 0.9999999... does equal 1 which has already been proving numerous times.

[verena]

Wrong. tanh^-1 is undefined for x>=1.

When x goes to infinity, tanh(x) approaches 1 but it is never equal to 1.

Do you believe what someone else wrote on the internet, as "proof" ?

This is all about confusing limits with equalities. Shortcut type of american "science".

It is just as easy to find a reference that says that tanh^-1 is undefined for x=1

[kucalc]

Do you believe what someone else wrote on the internet, as "proof" ?

I normally wouldn't, but Wolfram is the most trusted mathematical source on the internet. Look at it's sources and references on the bottom of the page and read those books if you don't believe.

This is all about confusing limits with equalities. Shortcut type of american "science".

That's pathetic. Stop blaming others for your problems and start showing us the proof.

The definition of tanh^-1 of x = 0.5[ln(1+x)-ln(1-x)]. Every source says that.

Thus if you plug in 1, 0.5[ln(2)-ln(0)]. ln(0) is negative infinity, but because of subtracting becomes positive infinity which is why tanh^-1 = infinity.

ln(0) is not undefined. It's negative infinity:
http://answers.yahoo...11104832AAWDqJ1
http://answers.yahoo...05123007AAMtOCj
http://mathforum.org...a...40&tstart=0

and I could cite another 20 textbooks written from around the world and get another 300 web pages confirming this.

[verena]

1) you don't believe.

2) show us the proof.

3) The definition of tanh^-1 of x = 0.5[ln(1+x)-ln(1-x)]. Every source says that.

4) ln(0) is negative infinity,

http://answers.yahoo...11104832AAWDqJ1
http://answers.yahoo...05123007AAMtOCj
http://mathforum.org...a...40&tstart=0

and I could cite another 20 textbooks written from around the world and get another 300 web pages confirming this.

1) Believing you can do in the church. Wolfgang seems the kind of authority that a couple hundred years ago put people in prison for saying that the earth is not flat. He should go back to school to freshen his knowledge about limits up. Please give him my greetings and send him: "Hallo Du Wolfgang, geh mal zurueck in die Realschule um Deine Limitenmathematik wieder aufzufreschen !"

2) I did, with a simple transformation using the arctangent hyperbolic, stated that

ATANH (0.99999....) = infinity, and ATANH(1) = undefined, therefore 1 <> 0.99999...

3) OK..

4) Wrong again. The limit of ln(x) with x going to 0 is negative infinity, that doesn't mean that ln(0) equals negative infinity, even when half the world thinks so in order to "fill the hole". Again, shortcut type of american "science". Oversimplification.

You are familiar with infinity, but you seem to have trouble to accept the concept of "undefined".

For your information:

ln(0) is Undefined. Ain't There. Does Not Exist.

-

I on my part, still have to see proof that 1 equals 0.999999.....

All I have seen presented is some crackpipe math using non-real numbers as real numbers, and drawing fantasy conclusions from it.

"10 x 0.999999999... = 9.9999999 etc. " is nonsense math, you cannot operate on mixed real and non-real numbers and then present calculations with them as real numbers.

"1/3 = 0.33333333... and 3 x 1/3 = 1 = 3 x 0.33.... = 0.99.... etc. thus " also nonsense, the 0.3333... is never equal to 1/3, just an approximation, and also a non-real number.

Actually, presenting a non-real number (0.99999...) and then stating that is is equal to a real number (1), is nonsense by itself. And that is the bottom line.

[kucalc]

Wolfgang seems the kind of authority that a couple hundred years ago put people in prison for saying that the earth is not flat. He should go back to high school to freshen his knowledge about limits up.

Have you not been reading the links I've been showing you? It's Wolfram, not Wolfgang. And he's still alive and he's a famous mathematician. Read before you argue and make a fool out of yourself.

Stephan Wolfram is a British mathematician (NOT a American), physicists and creator of the legendary Mathematica Computer Algebra System (which is used by professional engineers and scientists). He's done work in theoretical particle physics, cosmology, cellular automata and in complexity theory.

His company, Wolfram Research International (which includes hundreds of mathematicians, scientists, engineers and physicists around the world) publishes their information and notes at Wolfram Online/MathWorld (again here is the link: http://mathworld.wol...licTangent.html). That's why I trust that source. Plus you can also verify by looking and reading the books listed below. Even the GNU Foundation (look up atanh()) and also the IEEE (the largest engineering society in the world) accept tanh^-1 of 1 to be infinity.

Read about him: http://en.wikipedia....Stephen_Wolfram

So who should we trust? You (verena) or 300+ mathematicians at Wolfram Research + IEEE + GNU + millions of mathematicians around the world? I don't think Stephan Wolfram needs to go back to highschool, you do. He's contributed more to mathematics than you have ever done in your life.

"1/3 = 0.33333333... and 3 x 1/3 = 1 = 3 x 0.33.... = 0.99.... etc. thus " also nonsense, the 0.3333... is never equal to 1/3, just an approximation, and also a non-real number.

Sorry, but I have to admit this must the stupidest thing I have ever heard. So is pi not a real number then because it has infinite digits? 1/3 is 0.3333..., it's not an approximation. 0.3333... and pi are real numbers. 0.33333... is a rational number, and rational numbers are a subset of real numbers.

EDIT: Talking with a couple of friends, it seems that you are using the small number line system, versus the Extended Real Number Line System (Click Here) which adds negative infinity or infinity. Because of this tanh^-1 behaves differently depending on which number line system is being used. However, you are still wrong because you mixed the two different number systems in order to make it look like 0.999999... does not equal 1. You have to choose one number system and stick to it. The correct values depending on what number system is used:

Elementary real number line (infinity does not exist):
tanh^-1 (0.99999....) = undefined
tanh^-1 (1) = undefined
ln (0) = undefined

Extended real number line (infinity is added):
tanh^-1 (0.999999....) = infinity
tanh^-1 (1) = infinity
ln (0) = negative infinity

Thus still proving that 0.999999... = 1.

Plus another problem is not only do you assume that 0.9999... does not equal 1, you think 0.999999.... is less than 1. The problem is, you must first prove 0.999999... is less than 1 before plugging it into a function (such as tanh^-1). You can't just say "oh since I'm assuming that 0.99999... is less than 1, when I plug in 0.99999.... into tanh^-1 the answer is different than tanh^-1 of 1" Of course they will be different if you assume 0.99999.... is less than 1. But, how do you know 0.99999... is less than 1? You must first prove that 0.9999.... is less than 1, which again, has never been shown. Until you have proven 0.999999... is less than 1, you can't show that tanh^-1 of 0.99999.... is different than tanh^-1 of 1, because it's possible that 0.99999... is equal to 1 unless shown that 0.9999.... is less than 1.

[verena]

Have you not been reading the links I've been showing you? It's Wolfram, not Wolfgang. And he's still alive and he's a famous mathematician. Read before you argue and make a fool out of yourself.

Stephan Wolfram is a British mathematician (NOT a American), physicists and creator of the legendary Mathematica Computer Algebra System (which is used by professional engineers and scientists). He's done work in theoretical particle physics, cosmology, cellular automata and in complexity theory.

His company, Wolfram Research International (which includes hundreds of mathematicians, scientists, engineers and physicists around the world) publishes their information and notes at Wolfram Online/MathWorld (again here is the link: http://mathworld.wol...licTangent.html). That's why I trust that source. Plus you can also verify by looking and reading the books listed below. Even the GNU Foundation (look up atanh()) and also the IEEE (the largest engineering society in the world) accept tanh^-1 of 1 to be infinity.

Read about him: http://en.wikipedia....Stephen_Wolfram

So who should we trust? You (verena) or 300+ mathematicians at Wolfram Research + IEEE + GNU + millions of mathematicians around the world? I don't think Stephan Wolfram needs to go back to highschool, you do. He's contributed more to mathematics than you have ever done in your life.

Oh, I see. Wolfram is English. That explains a lot. The English are well known for their great sense of humour, and they appreciate a good comic with a clever joke.

And I also see now, that one of Wolfram's contributions is to recognize infinity as a 'extended' real number. According to him, infinity exists, and you can work with it. Then, ln(0) is simply equal to minus infinity. And thanks to him, now 'zero' is added to the logarithmic scale.

You see, the type of math that I learned, teaches that infinity is not a real number, it does not exist, and can never be reached. It requires so-called 'abstract thinking'. You have to imagine something that does not exist, that you go towards, and that you never reach. Also, that math says that some things simply do not exist, but can only be approached. Like the logarithm of zero. You can only go towards it, but never reach it. And because infinity is not accepted as a real number, you can not say "ln(0)=-∞", because it is considered illegal to equate a real number (0) to a something not real (∞). Therefore, ln(0) is "undefined" - yet another hard thing to understand. "You mean, you can get almost infinitely close to zero, but you have to exclude zero itself ?" Many people gave up on math because of these difficult mental requirements.

But now, thanks to Wolfram, 'abstract thinking' is no longer required, and there is a lot less 'undefined'. He really brings the "fun" back in mathematics. Infinity can just be treated like any other real number. Now, you can just say, well, the logarithm of zero is equal to minus infinity.

This implies, by the way, that e^(-∞)=0, apparently "Wolfram's definition of zero".

I wish I had witnessed the introduction of this new definition of zero at the British Royal court. "My Mind" oracled Wolfram, "My Mind... has reached.... Infinity! Not only, Positive Infinity, - but also... Negative Infinity! And, guess what - Both Infinities Exists ! They Are Real !!". At which point the younger British princes started giggling and snickering -they had just learned in school that you can never reach infinity, and understood the concept.
Wolfram continued: "And, Your Highnesses, at Negative Infinity, which is even further away than New Zealand at the other side of the Earth, at Negative Infinty - my Mind received the insight, that when you take the 'Exponent' of negative infinity..." (here, also prince Charles started laughing out loudly, because he already had an idea what was coming) "...when you exponentiate negative infinity, you get a number that is sooooo frikkin' unbelievably small...... that it is essentially, absolutely, I'm tellin' ya, definitely and simply, equal to...... zero !!!!"

At this point, the entire British Royal court started shaking with laughter so loud that the windows in Buckingham Palace were rattling. The tears were rolling over Queen Elizabeth's cheeks as she thought "What a NONSENSE - that guy is FUNNY, Wolfram is just the best court jester I have ever seen!"

Correction, not the entire British court was amused. Princess Diana seemed to be in some kind of shock and was talking to her butler: "Paul, that blithering idiot is just declaring the utmost horrible mathematical nonsense, and they are all LAUGHING about it, they think it it FUNNY ! It is Terrible ! Get me a ticket to Paris and call Dodi that I'm on my way, I need to see some normal people and can't wait to get away from this craziness."

(will be continued)

[kucalc]

Oh, I see. Wolfram is English. That explains a lot. The English are well known for their great sense of humour, and they appreciate a good comic with a clever joke.

What is your problem? First America, now Britain? You might as well make fun of Sir Issac Newton, Alan Turing or Andy.Davis (another Admin here) because they're British as well. You think your race is better than everyone? I can now see more clearly that you judge people on their race and such. Intelligence has nothing to do with race, so stop with this "American math" or "British humor". There is no such thing as that. You (verena) are the problem. It's your own racists beliefs that are preventing you from becoming more knowledgeable.

I also find your long story making fun of Wolfram disrespectful, useless and of no mathematical value to the topic or conversation. All I did was explain why MathWorld was a trustable source, because Wolfram is a well known mathematician and you doubted it.

Now let's talk about math and no more of this race stuff:

Forgot about the infinity thing, it doesn't have anything to do with proving 0.999999..... does not equal 1. What matters is that no matter what number system we are using, tanh^-1 (0.99999....) DOES equal tanh^-1 (1). Show us the proof that 0.999999... is less than 1 first. If you prove 0.9999999... is less than 1, then you prove that tanh^-1 (0.99999....) does not equal tanh^-1 (1). You can't go the other way around, because you haven't determined what 0.9999999.... is yet (is it 1 or not? less than 1 or equal?). The only proof available shows that 0.999999... is not less than or greater than 1, thus it must be 1.

Whether we use the basic real number line (which you use): tanh^-1 (0.999999.....) = tanh^-1 (1) = undefined
Or the extended real number line (which everyone else uses): tanh^-1 (0.99999999.....) = tanh^-1 (1) = infinity

Also, Wolfram wasn't the first guy to add infinity to the number line. It was already thought of even before calculus, hundreds of years ago. In fact, some believe that by doing so, it helped lead to the creation of calculus.

I'm getting the impression that you aren't taking a look at the links and text I have listed. The stuff you're saying is just ridiculous. You've proven already that you have a very limited understanding of basic math. You say 0.33333... is not a real number? It is a real number. Even a 6 or 7 year old child knows that: Real Numbers Also, you didn't even know what the extended real number line is.

So I'll ask this only once again, show us first that 0.999999... is less than 1.

[verena]

1) I maintain that: tanh^-1 (0.999999.....) = infinity
This is perfectly legitimate in the basic real number line, because both 0.9999... and infinity are non-real numbers. No mixing of number types.


2) About 0.333333....: I only meant to say that 0.333333 is not a PURE real number. It is only a RATIONAL real number.
Back in the 17th century, when 0.33333... was introduced as a APPROXIMATION of the real number 1/3, the 'real number' mathematicians had trouble accepting it into the collection of real numbers, because it essentially is a NON-REAL NUMBER - it never ends, just 3s towards infinity. After some discussion, and being reasonable (rational) people, they did allow to to exist along with the PURE real numbers (like: 8, 18.4, 1/7), but only in the SUBSET of RATIONAL numbers. "SUB" means "LOWER" and "RATIONAL" means "REASONABLE". Being in the "SUB" set, 0.33333.... is always inferior to the fraction 1/3 (Now, you are going to call me racist again aren't you?). Also, because it is a RATIONAL number you have to excersize REASON (=use your brain) to work with it in a responsible way. The 17th century mathematicians gave us plenty of warnings and "caution" flags along with 0.33333.... to signal that it is NOT exactly equal to 1/3, but it goes in its own class as its own type of number. You understand ?

ONLY WHEN your brain works at the level of the dollar store calculator,
(you know, 1 / 3 x 3 = [0.9999999]) will you use 0.3333... x 3 as 'proof' that 0.9999... = 1. Just conveniently ignore that, as a mathematician, your duty is to use *good reasoning* to perform calculations with this rational number 0.33333...... rather than with the 'pure' real number 1/3.

3) Quote kucalc "you didn't even know what the extended real number line is."

No, and I'm very happy with that, I see that Wolfram has introduced a lot of nonsense to math. And I'm having a lot of fun pointing out the consequences of his 'work'.

4) Quote kucalc: "So I'll ask this only once again, show us first that 0.999999... is less than 1."

I already have told you that 0.9999999.... is a non-real number, and 1 is. They are not equal. You have not provided any argument against my statement.

To answer your question, and only because it is the last time you ask it:
(proof start) You know that 0.9 + 0.1 = 1, and that 0.9999999 + 0.0000001 = 1.
As you add nines to the one term of this equation, you have to insert zeroes into the other term of the equation.
As certain as you will NEVER reach infinity (keep adding nines) you will ALWAYS insert zeroes and there will ALWAYS be a little difference between 0.9999..... and 1.
(proof end).

In your 'modern' extended number line, once you reach infinity, all of a sudden "OOPS' the difference is gone ! Now, we have 1.0 which is essentially exactly the same as the dollar store calculator's 0.9999999 !!!

5) I know that you have been DYING for me to say "there is no number between 0.999999.... and 1" because you would have jubilantly jumped up and said "SEE? there is nothing between them, therefore you have just said yourself that they are equal because the difference is nothing, zero" but I cannot say that because infinity is never reached, and I would be comparing a non-real number to a real number. What I CAN say is that 0.999999 extended to infinity is as close to 1 as you can get, without ever reaching 1.

6) Also I know that you have been WAITING all along for me to say "um, the difference between 0.999999... and 1 is simply 10^(-∞) "
because 10^(-∞) is the SECOND and IMPROVED Definition of ZERO by Wolfram !!! Remember I already have pointed out the idiocy of his first definition of zero e^(-∞) with my little story about its introduction at the British Royal Court above. 10 is bigger than e, so zero is 'reached' even faster with 10^-∞ than with e^-∞. You can show this on any scientific calculator, but mathematically, ha ha what a nonsense !

7) Bottom line: Thank you for introducing me to the 'extended number line' and the so-called "improvements" of math by Wolfram. Thanks to Wolfram, 0.9999999 is now equal to 1, so no child is left behind, even when they can only afford a dollar store calculator.

Thanks to Wolfram, and you have made it perfectly clear to me, all you need now to become a mathematician like you, is a dollar store calculator brain.

[kucalc]

Now before you start, make sure you understand and read everything:

(proof start)
As certain as you will NEVER reach infinity (keep adding nines) you will ALWAYS insert zeroes and there will ALWAYS be a little difference between 0.9999..... and 1.
(proof end).

Hahaha, you criticize me for being abstract, yet this proof is kind of abstract. How can you have a difference, if you ALWAYS insert zeroes for eternity? There, you said it yourself. 1 also has infinity zeroes (1.0000000....). If you ALWAYS insert zeroes as you can never reach infinity (as a human), thus never inserting the 1.

1) I maintain that: tanh^-1 (0.999999.....) = infinity

Plus also tanh^-1 (1) = infinity if using the extended real number line system.

1) I maintain that: tanh^-1 (0.999999.....) = infinity
This is perfectly legitimate in the basic real number line, because both 0.9999... and infinity are non-real numbers. No mixing of number types.

You justify that 0.99999.... is a non-real because of infinite digits? Now this must be the stupidest thing I've ever heard. Is this how you justify your proof? Only an idiot would do that. 0.99999.... just has infinite digits, it's not infinity, just like pi or square root of 2 or maybe they didn't teach you pi yet in school.... Then according to you, 1 must also be a non real number also because 1 has repeating zeros (infinity zeroes or 1.000000....). Then, that must also mean according to you, all numbers are non real. Again, numbers with repeating decimals are real.

The 17th century mathematicians gave us plenty of warnings and "caution" flags along with 0.33333.... to signal that it is NOT exactly equal to 1/3, but it goes in its own class as its own type of number. You understand ?

This sounds like your just pulling this out of your ass. Where is your reference? You're telling me a story which you probably might be making up filled with abstract ideas, and you want me to believe it? Give me a textbook or a link to a web page. You haven't given us a single reference, whereas I have millions of references to back up what I'm saying. 0.333333.... is not in it's own class. You have failed to show us an example when 0.333333.... does not equal 1/3. When 0.333333.... fails to be an equivalent of 1/3, then you're getting somewhere. Every fraction has a decimal equivalent. What is 1/3 decimal's equivalent? In fact, that's why fractions were invented, not only to describe parts of a whole, but so we don't have to right out repeating decimals.

ONLY WHEN your brain works at the level of the dollar store calculator,
(you know, 1 / 3 x 3 = [0.9999999]) will you use 0.3333... x 3 as 'proof' that 0.9999... = 1. Just conveniently ignore that, as a mathematician, your duty is to use *good reasoning* to perform calculations with this rational number 0.33333...... rather than with the 'pure' real number 1/3.

Hehehe, it's funny that you compare me to a calculator. In fact, it's actually you who first wanted to use our CASIO calculators to to prove 0.999999.... does not equal 1, so who's the one with brain of a "dollar store calculator"? You. Me on the other hand, I have never used a calculator to prove 0.99999999..... equals 1, because a calculator can't hold infinite digits. Just like a "dollar store calculator", you don't see that number can have infinite digits. Ever heard of pi? Or square root of 2?

7) Bottom line: Thank you for introducing me to the 'extended number line' and the so-called "improvements" of math by Wolfram. Thanks to Wolfram, 0.9999999 is now equal to 1, so no child is left behind, even when they can only afford a dollar store calculator.

I already said, Wolfram didn't invent the extended number line. It was already invented before calculus was invented. Why won't you read!?!? If you're not going to read, you're just making a fool out of yourself.

[verena]

Here is my proof that 0.99999... is less than 1:

(proof start)

You know that 0.9 + 0.1 = 1, 0.99 + 0.01 = 1, and that 0.9999999 + 0.0000001 = 1, etc.
As you add nines to the first term of this equation, you insert zeroes into the second term of the equation. The sum always being 1.
As certain as you will NEVER reach infinity (keep adding nines) you will ALWAYS insert zeroes and there will ALWAYS be a little difference between 0.9999..... and 1.
(proof end).

Here is kucalc's reaction:

Hahaha, you criticize me for being abstract, yet this proof is kind of abstract. How can you have a difference, if you ALWAYS insert zeroes for eternity? There, you said it yourself. 1 also has infinity zeroes (1.0000000....). If you ALWAYS insert zeroes as you can never reach infinity (as a human), thus never inserting the 1.

I have never criticized anyone for being abstract. Actually I would appreciate if you would show to be capable of some abstract thinking.

Your story throughout this thread looks like, and please correct me if I'm wrong:
"once I have inserted "infinity" zeroes between the decimal point and the "1" of the second term, that annoying little "1" to the right or at the end of the infinity zeroes will be beyond the infinity zeroes and essentially have disappeared and we can forget about it".