2 Questions Regarding Integrals
#1

Posted 24 February 2010 - 02:19 PM
#2

Posted 24 February 2010 - 05:25 PM
Hi is it possible to find integrals enclosed along the y axis?, and can you find indefinite integrals in the graph mode. Thx
#3

Posted 25 February 2010 - 12:58 AM
Integrals enclosed along the y axis? Please explain what you mean by that.
What i mean is finding the area enclosed by the function and the y axis
For example for the function y=x^2
If the area is enclosed by the x axis it would be like this
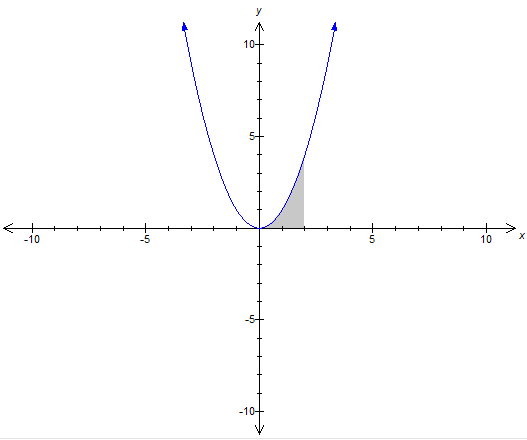
and if the area is enclosed by the y axis it would be like this
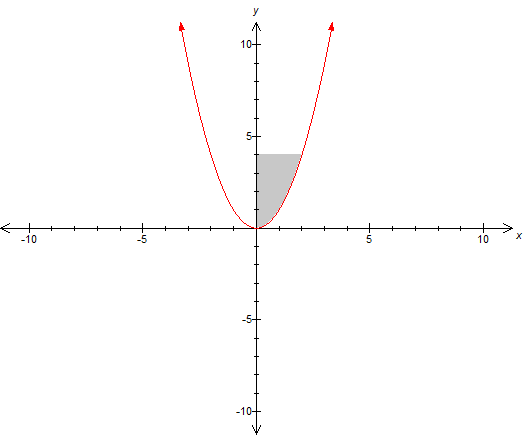
#4

Posted 25 February 2010 - 05:58 AM
2. calculate the area under the curve according to Newton' formula- see your first picture
3. subtract these 2 areas for getting the result as seen on your second picture
#5

Posted 25 February 2010 - 11:05 AM
1. calculate the rectangular area S = (x2-x1)*(y2-y1)
2. calculate the area under the curve according to Newton' formula- see your first picture
3. subtract these 2 areas for getting the result as seen on your second picture
Is there a way to type it into a casio classpad
#6

Posted 25 February 2010 - 03:38 PM
2. store the lower and upper limits to variables- e.g. a and b, this step is optional, you can use numeric input instead of using the variables
3. type [(b-a)*(f(
or type directly [(5-1)*(f(5)-f(1)] - INT(f(x), 1, 5, x)
4. press "exe" button
If the result is negative (S<0), use "abs" function to correct this.
edited: why there is a smile instead of function value in point b? test: f(a), f(
Edited by pan.gejt, 25 February 2010 - 03:44 PM.
#7

Posted 25 February 2010 - 05:01 PM
Is there a way to type it into a casio classpad
you can find an inverse of that function and integrate from x = 0 to 4.
In the classpad, you swap x and y. Then you solve for the new y.
Then plug in the function.
#8

Posted 26 February 2010 - 02:21 AM
edited: why there is a smile instead of function value in point b? test: f(a), f(
[/quote]
#9

Posted 26 February 2010 - 04:46 AM
Finding the inversion function is not simple and sometimes the inversion function does not exist (in most cases).
Using INT(y^2, 1, 5, y) does not solve the situation, because the integration is still in terms of "x" and not "y"
if the inversion function exists you should recalculate the lower and upper limits and integrate the inversion function
e.g. for function f(x)=x^2 :
lower limit a=1 therefore y(a)=1
upper limit b=5 therefore y(
so integration in case of function shown above should be between 1 and 25.
#10

Posted 26 February 2010 - 04:25 PM
my comments:
Finding the inversion function is not simple and sometimes the inversion function does not exist (in most cases).
Using INT(y^2, 1, 5, y) does not solve the situation, because the integration is still in terms of "x" and not "y"
if the inversion function exists you should recalculate the lower and upper limits and integrate the inversion function
e.g. for function f(x)=x^2 :
lower limit a=1 therefore y(a)=1
upper limit b=5 therefore y(=25
so integration in case of function shown above should be between 1 and 25.
#11

Posted 26 February 2010 - 11:21 PM
#12
 Guest_VasiLisa_*
Guest_VasiLisa_*
Posted 02 January 2011 - 12:23 PM
Я новичок. Помогите кто знает, как загрузить картинку (UserBar) в подпись?
Никак не пойму.
Как я поняла, здесь можно загрузить картинку только по ссылке на другом сайте, а как загрузить ее со своего компьютера?
У меня есть красивая картинка-UserBar на компьютере, хочу его закачать, но не понимаю как...
#13

Posted 02 January 2011 - 03:17 PM
You need to upload it to some kind of website. You can't upload it directly from your computer to the forum - that can only be done with avatars.Всех с Новым годом!
Я новичок. Помогите кто знает, как загрузить картинку (UserBar) в подпись?
Никак не пойму.
Как я поняла, здесь можно загрузить картинку только по ссылке на другом сайте, а как загрузить ее со своего компьютера?
У меня есть красивая картинка-UserBar на компьютере, хочу его закачать, но не понимаю как...
Also, you're in the wrong topic (and in the wrong language...) I had to use an automatic translator to read, so my answer may not be completely relevant to your question.
#14
 Guest_VasiLisa_*
Guest_VasiLisa_*
Posted 02 January 2011 - 08:16 PM
Всем спасибо за помощь
1 user(s) are reading this topic
0 members, 1 guests, 0 anonymous users














